1560 - Η έννοια της πρόβλεψης στη θεωρία ωφέλειας/χρησιμότητας
Ν. Λυγερός
Για να αποδειχθεί η ύπαρξη μιας ικανοποιητικής συνάρτησης ωφέλειας/χρησιμότητας χρειαζόμαστε τις εξής συνθήκες κατά την προσέγγιση των von Neumann και Morgenstern .
- Ένα άτομο στο οποίο προσφέρονται δύο προβλέψεις μπορεί να αποφασίσει ποια είναι η προτιμότερη ή εάν είναι το ίδιο επιθυμητές.
- Η ταξινόμηση των προτιμήσεων που προκύπτει είναι μεταβατική.
- Έστω ότι ξεκινάμε με δύο καταστάσεις εξίσου επιθυμητές. Κάθε συνδυασμός πιθανοτήτων αυτών των καταστάσεων θα είναι εξίσου επιθυμητός όσο η καθεμιά ξεχωριστά.
- Εάν Α>Β>Γ τότε υπάρχει ένας συνδυασμός πιθανοτήτων των Α και Γ που είναι το ίδιο επιθυμητός με το Β. Αυτό ισοδυναμεί με μια υπόθεση για τη συνέχεια.
- Εάν 0
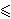 p
p 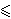 1 και Α και Β είναι το ίδιο επιθυμητές, τότε οι pΑ+(1– p)Γ και pΒ+(1– p)Γ είναι το ίδιο επιθυμητές. Επίσης αν Α και Β είναι το ίδιο επιθυμητές, τότε η Α μπορεί να αντικατασταθεί από τη Β σε οποιαδήποτε σχέση διάταξης επιθυμιών η οποία ικανοποιείται από τη Β.
1 και Α και Β είναι το ίδιο επιθυμητές, τότε οι pΑ+(1– p)Γ και pΒ+(1– p)Γ είναι το ίδιο επιθυμητές. Επίσης αν Α και Β είναι το ίδιο επιθυμητές, τότε η Α μπορεί να αντικατασταθεί από τη Β σε οποιαδήποτε σχέση διάταξης επιθυμιών η οποία ικανοποιείται από τη Β.
Πρέπει να παρατηρήσουμε ότι αυτή η συνάρτηση ωφέλειας/χρησιμότητας αν και υπάρχει, δεν είναι μοναδική αφού κάθε γραμμικός μετασχηματισμός είναι και αυτός μία συνάρτηση ωφέλειας/χρησιμότητας.
Συνεπώς η συνάρτηση u έχει τις εξής ιδιότητες:
- u (Α) > u (Β) ισοδυναμεί με το ό,τι η Α είναι προτιμότερη από τη Β.
- Αν 0
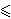 p
p 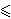 1 τότε u [pΑ+ (1– p)Β] = p u (Α) + (1– p) u (Β).
1 τότε u [pΑ+ (1– p)Β] = p u (Α) + (1– p) u (Β).
Αυτή η γραμμική ιδιότητα είναι πολύ σημαντική διότι επιτρέπει τη δομική μεταφορά του συστήματος και την εφαρμογή μέσω της θεωρίας του Nash , του θεωρήματος του σταθερού σημείου.
Το πλαίσιο αυτό μπορεί να φανεί απλοϊκό διότι προϋποθέτει ότι έχουμε μια πλήρη γνώση όλων των δυνατοτήτων και των κινήσεων. Η καινοτομία του Nash προέρχεται όμως από τη μη συμβατική προσέγγιση του συστήματος που αποτελούν οι συνθήκες. Ενώ ο von Neumann και ο Morgenstern το εξέταζαν ως ένα κλειστό σύστημα που προσεγγίζει την τελειότητα, ο Nash το είδε ως μία ανοικτή δομή που προσεγγίζει την πραγματικότητα της διαπραγμάτευσης. Το ίδιο σύστημα με ένα άλλο βλέμμα μπορεί να χρησιμοποιηθεί αποτελεσματικά για προβλήματα που όχι μόνο δεν είχαν λύση αλλά που δεν μπορούσαν να τεθούν. Το εργαλείο της πρόβλεψης και της ωφέλειας/χρησιμότητας υπήρχε, ήταν όμως απαραίτητη μια διαφορετική σκέψη. Οι αρχές της θεωρίας παιγνίων είχαν την τάση να οδηγούν τους ερευνητές στην αναζήτηση της τέλειας γνώσης. Ενώ η νοοτροπία και στην ουσία η νοοστρατηγική του Nash έχει ως βάση την αποδοχή της μη ολικής γνώσης και την αντιμετώπισή της με έναν μη συμβατικό τρόπο. Αυτό εξηγεί πώς κατάφερε να δημιουργήσει την έννοια της ισορροπίας εφόσον η βάση της είναι η συμμετρία της μη γνώσης.
