21 - Sur une courbe continue de longueur finie non dérivable en une infinité dense de points
N. Lygeros
Introduction
Dans l’ensemble des fonctions exotiques il existe actuellement deux catégories :
– les fonctions irrégulières continues n’admettant presque nulle part de dérivées (voir S.Dubuc [1]).
– les fonctions singulières : continues, croissantes et dont la dérivée est presque partout nulle. L’appellation est de H. Lebesgue (voir G. de Rham [2]).
Voici un commentaire de H. Poincaré, sur une liste de fonctions irrégulières – comme celle de F. Weierstrass [3] ou celle de C. Cellérier [4], ( que l’on peut considérer respectivement comme la partie réelle et imaginaire d’une fonction complexe ) lesquelles sont, comme l’a montré G.H. Hardy [5], dépourvue de dérivées – mais qui aurait pu être adressé à l’ensemble des fonctions exotiques :
“Autrefois, quand on inventait une fonction nouvelle, c’était en vue de quelque but pratique; aujourd’hui on les invente tout exprès pour mettre en défaut les raisonnements de nos pères et on n’en tirera jamais que cela.” [6]
Même si H. Poincaré avait raison, bien qu’à présent de nombreuses applications sont là pour contredire ses propos, et que la seule contribution de ces fonctions serait d’anéantir certains “raisonnements” alors nous pensons qu’elle justifierait entièrement leur existence.
C’est sans doute G. de Rham qui a été le premier à exhiber une propriété allant dans le sens d’une unification de ces deux grandes catégories, en établissant que certains de leurs éléments respectifs pouvaient être générés à partir d’une même équation fonctionnelle paramétrée ( voir [7]). De plus il a réussi à retrouver avec cette méthode un exemple exotique qui lui est propre et qu’il avait obtenu uniquement à l’aide d’un procédé géométrique simple.
De Rham en généralisant son exemple obtient une courbe continue qui a un ensemble dense de points anguleux ( voir [8] ). Mais ce qui est vraiment important dans le cadre d’une mentalité fractale (voir [9]) c’est la longueur de cette courbe : elle est finie !
En interprétant le résulta de G. de Rham, à notre façon, l’on peut dire qu’il a montré le théorème suivant : il existe une courbe continue de longueur finie qui n’est pas dérivable en une infinité de points.
Notre idée alors, puisque nous savions qu’un tel être pouvait exister, fut d’en construire un tout aussi élémentaire mais dont la géométrie suffisait à elle seule – contrairement à l’exemple de de Rham – pour montrer qu’il vérifiait bien le théorème précédent; en d’autres termes nous voulions que sa propriété soit aussi évidente à montrer que celle que possède la courbe de von Koch [10] à savoir qu’elle n’a pas de dérivée.
Description de la construction
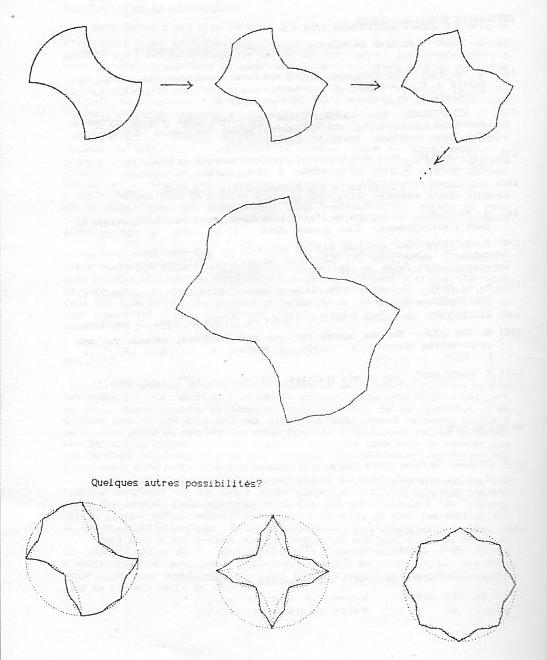
Considérons l’arc d’un cercle – que nous supposerons centré à l’origine d’un repère – qui se trouve dans le premier cadran d’un plan. Nous procédons alors à une symétrie orthogonale de cet arc par rapport à sa corde. Ensuite nous faisons tourner dans le sens rétrograde l’arc ainsi obtenu, dont nous avons fixé l’extrémité qui était sur l’axe des abscisses, jusqu’à ce que l’autre extrémité qui était sur l’axe des ordonnées retouche le cercle initial. Nous agissons de même avec le nouvel arc mais cette fois nous fixons l’extrémité que nous avions déplacée précédemment.
En répétant 3 (=2²-1) fois cette procédure, la toute première extrémité que nous avions bougée, se retrouve à sa place initiale, et la figure obtenue de cette façon représente le premier itéré de notre exemple. À présent pour obtenir le deuxième ensemble itéré nous faisons cette fois une symétrie orthogonale par rapport à la corde de l’arc dont l’une des extrémités se trouve sur l’axe des ordonnées et l’autre est le milieu de l’arc – qui st le premier cadran – du premier ensemble itéré. Ensuite de la même façon que précédemment nous tournons l’arc obtenu et nous répétons 7 (=23-1) fois cette opération; obtenant ainsi le deuxième ensemble itéré.
En procédant de cette façon une infinité de fois on construit un être mathématique qui est une courbe continue (par construction), de longueur finie (elle est égale à celle du cercle initial, en effet étant donné que nous n’avons utilisé que des isométries nous conservions à chaque itération la longueur), et non dérivable en une infinité de points (puisque chaque fois que nous créons une cassure au milieu d’un arc notre méthode conserve pour toutes les étapes ultérieures l’angle ainsi formé et il est trivial de montrer que cet angle n’est jamais plat).
Remarques
Il est aisé de montrer que la dimension de Hausdorff de notre courbe est égale à 1. Ce résultat a le mérite de montrer la cohérence, d’une part de cette étude puisque la longueur est la mesure de la dimension 1 et d’autre part de nos affirmations, quant à l’appartenance de notre courbe à un nouveau genre de courbes; en effet bien que B. Mandelbrot refuse de donner une définition mathématique des fractals l’on peut dire sans se tromper que ces derniers vérifient la propriété suivante : leur dimension topologique est strictement inférieure à leur dimension fractale.
Ainsi dans l’ensemble des courbes planes bornées l’exemple de de Rham (points anguleux) et le nôtre (demi-tangentes différentes) apparaissent comme des courbes intermédiaires entre les courbes classiques (de longueur finie, n’ayant qu’un nombre fini de points où elles ne sont pas dérivables) et les fractals classiques (de longueur infinie, dérivables nulle part).
Comme cela s’est produit avec l’exemple de von Koch qui à la suite de la généralisation de Mandelbrot [11] a donné naissance à la notion d’autosimilarité, nous pensons que notre méthode de construction, une fois généralisée sans doute, engendrera une nouvelle notion tout aussi importante pour ce nouveau genre de courbes.
Références bibliographiques
[1] S. DUBUC : Modèles de courbes irrégulières. dans Fractales , Masson 1987, p. 16-43.
[2] G. de RHAM : Sur certaines équations fonctionnelles. dans l’ouvrage publié à l’occasion de son centenaire par l’ École Polytechnique de l’ Université de Lausanne (1853-1953) , p. 95-97.
[3] F. WEIERSTRASS : Über kontinuirliche funktionen eines rullen arguments die für keinen werth des letzteren einen bestimmter differential quotienten besitzen. Mathematische werke 11, 1872, p. 71-74.