2377 - Η αξιοποίηση του λήμματος του Schwarz από τον Κ. Καραθεοδωρή
N. Lygeros
Ένα από τα χαρακτηριστικά του Κ. Καραθεοδωρή στον τομέα της ανάλυσης είναι η έννοια της θεμελίωσης. Δεν του αρκεί η μελέτη ενός τομέα. Χρειάζεται να εξετάσει τα θεμέλιά του και μάλιστα να επανεξετάσει την ιεραρχία των θεωρημάτων από μία νέα οπτική γωνία, όπως γίνεται με το παράδειγμα του λήμματος του Schwarz. Στην εποχή του, όλοι αποδέχονταν ότι ήταν ένα βασικό λήμμα για τη θεωρία. Όμως ο Κ. Καραθεοδωρή απέδειξε επιπλέον ότι είναι ουσιαστικό. Ένα ολόκληρο κεφάλαιο στα βιβλία του έχει το λήμμα του Schwarz ως τίτλο. Μέσω του αποδεικνύει πρώτα τη μοναδικότητα της σύμμορφης απεικόνισης μιας απλής συνεκτικής περιοχής. Δείχνει επίσης ότι το θεώρημα του Liouville είναι απλώς ένας συνδυασμός του λήμματος του Schwarz με πιο απλά θεωρήματα. Με την αναλλοίωτη μορφή του λήμματος δείχνει πώς συνεπάγεται το θεώρημα του Pick. Αλλά ένα από τα πιο εντυπωσιακά του σημεία είναι η μετατροπή του θεωρήματος του Harnack σε απλή επίπτωση του λήμματος του Schwarz. Διότι, όπως το γράφει και ο ίδιος ο Κ. Καραθεοδωρή, η θεμελιώδης σημασία του θεωρήματος του Harnack είχε αναγνωρισθεί προ πολλού. Όμως η μεθοδολογία που ακολουθεί ο Κ. Καραθεοδωρή το διαμορφώνει σε ένα απλό συμπέρασμα του λήμματος του Schwarz. Έτσι αποδεικνύει ακόμα μία φορά ότι η ουσία βρίσκεται σε αυτό το λήμμα και όχι στο αναγνωρισμένο θεώρημα. Όμως αυτό δεν επαρκεί για το πνεύμα του Κ. Καραθεοδωρή. Για να εμβαθύνει στην ουσία και τον θεμελιακό χαρακτήρα του λήμματος του Schwarz μελετά προεκτάσεις του: οι προεκτάσεις του λήμματος του Schwarz επιτρέπουν και την εύκολη απόδειξη του θεωρήματος του Julia. Και αυτή η απόδειξη προσφέρει μία γεωμετρική ερμηνεία του θεωρήματος του Julia. Ας επανέλθουμε, λοιπόν, στο ίδιο το λήμμα του Schwarz. Η απόδειξη που καταγράφεται στο κείμενο του Κ. Καραθεοδωρή είναι του Erhard Schmidt. Ο Κ. Καραθεοδωρή την είχε ήδη δημοσιεύσει στο άρθρο του με τίτλο: Sur quelques généralisations du théorème de M. Picard το 1905 στα Comptes Rendus de l’ Académie des Sciences (Paris). Μία ανάλογη απόδειξη είχε γίνει, όμως, και από τον H. Poincaré στο άρθρο του με τίτλο: Sur les groupes des équations linéaires το 1884 στα Acta Mathematica.
Για τους αναγνώστες δίνουμε την αγγλική εκδοχή του λήμματος του Schwarz όπως τη διατύπωσε ο ίδιος ο Κ. Καραθεοδωρή.
SCHWARZ’S LEMMA. If the analytic function f(z) is regular for 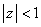 ,
,
if  for
for 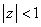 , and if further f(0)=0, then either
, and if further f(0)=0, then either
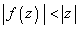 for
for 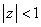
or f(z) is a linear function of the form 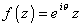 where θ is real.
where θ is real.
Με άλλα λόγια, είναι αξιοθαύμαστο το ό,τι ο Κ. Καραθεοδωρή καταφέρνει να αξιοποιήσει τόσο αποτελεσματικά ένα τόσο απλό λήμμα, τουλάχιστον φαινομενικά.
