3112 - Καταγραφή του μαθήματος Θεωρητικής Μηχανικής του Κ.Καραθεοδωρή
Ν. Λυγερός
Θεωρητική Μηχανική
Μάθημα του Μετσοβίου Πολυτεχνείου
Εισαγωγή
1. Η Μηχανική είναι η επιστήμη της κινήσεως, ερευνά
δηλαδή τους νόμους οίτινες διέπουν τας κινήσεις των σωμάτων
προς άλληλα.
Τας αρχάς επί των οποίων στηρίζεται το οικοδόμημα
της Μηχανικής θα εύρωμεν διά της μελέτης των απλουστέρων
κινήσεων αίτινες πραγματοποιούνται εν τη Φύσει και της
γενικεύσεως των πορισμάτων μας δια της μεθόδου της επαγωγής.
Η Μηχανική είναι λοιπόν Φυσική Επιστήμη ήτις βασίζεται
επί πείρας εν μέρει πάρα πολύ αρχαίας της οποίας τα ίχνη
ευρίσκομεν και εις αυτά ακόμη τα ομηρικά έπη, τα αξιώματα
όμως της Μηχανικής, δηλαδή αι αρχαί αίτινες επιτρέπουν την εφαρ-
μογήν των μεθόδων της μαθηματικής Αναλύσεως, εις τα
προβλήματα της κινήσεως είναι κτήμα σχετικώς νέον
της ανθρωπότητος. Αι ιδέαι τας οποίας είχεν π.χ ο Αριστο-
(~347π.Χ) τέλης περί κινήσεως των σωμάτων είναι καθ’ όλα άχρηστοι και
εσφαλμέναι πρώτος ο Αρχιμήδης (~ 250 π. Χ) κατώρθωσεν
να λύσει επακριβώς προβλήματα τινά της Μηχανικής.
Αλλά ως πατήρ της νεωτέρας Μηχανικής δύναται να
θεωρηθεί ο G. Galilei ( 1564 – 1642) του οποίου τάς έρευ-
νας εξηκολούθησαν ο Chr. Huyghens (1629 – 1695 ) και ο
I. Newton ( 1642 – 1727) όστις διετύπωσεν
το οριστικόν σύστημα των
αξιωμάτων της Μηχανικής.
- Χώρος. Ο προσδιορισμός των κινήσεων των
σωμάτων γίνεται δια συγχρόνων
μετρήσεων του χώρου και του χρόνου.
Τας μετακινήσεις ενός ορισμένου σώματος δεν δυνάμεθα
να παρατηρήσωμεν ει μη εν σχέσει πρός άλλο το οποίον
θεωρούμεν ακίνητον και του οποίου αι διαστάσεις μένουσι σταθε-
ραί.
Όταν έχομεν λάβει τοιούτον το σώμα δυνάμεθα να το
συνδέσωμεν ακλονήτως προς τρεις καρτεσιανούς άξονες των
συντεταγμένων καθέτους προς αλλήλους και ορίζομεν τότε τας
εκάστοτε θέσεις των σημείων τα οποία παρατηρούμεν δια
των συντεταγμένων αυτών.
Εν τη πράξει όμως υπολογίζονται
συνήθως αι καρτεσιαναί συντεταγμέναι αφ’ ου ορισθώσι αι
θέσεις των σημείων δι’ άλλων μεθόδων προσαρμοζομένων
καλλίτερα προς τας εκάστοτε περιστάσεις.
Ούτω πλοίον το οποίον θέλει να εξακριβώση την θέσιν
του σχετικώς προς την ακτήν καταμετρά δύο γωνίας
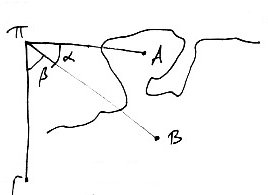
α, β τας οποίας σχηματίζουν αι
ακτίνες αι συνδέουσαι το πλοίον Π
μετά τριών γνωστών σημείων της στερεάς.
Η δε θέσις του πλοίου ευ-
ρίσκεται επί του χάρτου εν τη τομή
τριών γνωστών κύκλων.
Επίσης οι αστρονόμοι καθορίζουν δια της μετρή-
σεως αφ’ ενός μεν γωνιών αφ’ ετέρου δε του χρόνου
τας παρατηρήσεις της τροχιάς των πλανητών και σωμάτων εν
τω ηλιακώ συστήματι.
- Ποίον σώμα θα θεωρηθή ακίνητον
εξαρτάται εκ του προβλήματος το οποίον θέλωμεν
να μελετήσωμεν.
α. Όταν πρόκειται διά την λειτουργίαν της μηχανής
ενός ατμοπλοίου θεωρούμεν αυτό το πλοίον ως ακίνητον.
β. Δια τας πλείστας κινήσεις των σωμάτων επί της γής
θεωρούμεν τους άξονας ακλονήτως συνδεδεμένους μετ’ αυτής.
γ. Εις τίνας περιπτώσεις ως π. χ διά τάς κινήσεις των
γυροσκοπίων τα οποία εσχάτως μεταχειρίζονται αντί
πυξίδων ή δια του υπολογισμού της τροχιάς των βλημά-
των του πυροβολικού λαμβάνομεν υπ’ όψιν και την περιστρο-
φικήν κίνησιν της γης, άξονας δε διερχομένους δια του
κέντρου της γης ακλονήτως δε συνδεδεμένων μετά της σφαί-
ρας των απλανών.
δ. Εις την Αστρονομίαν τέλως λαμβάνομεν άξονας οίντινες
δεν είναι ακλονήτως συνδεδεμένοι μεθ’ ουδενός σώματος του
ηλιακού συστήματος και οι οποίοι ορίζονται μόνον δια
της ιδιότητος αυτών ότι δι’ αυτούς ισχύουν οι νόμοι του Νεύ-
τωνος.
Η τελευταία αύτη περίπτωσις μάς δίδει εν πρώτον παρά-
δειγμα αξόνων οι οποίοι συνδέονται προς ιδανικόν σώμα μη
έχον ουδεμίαν πραγματικήν υπόστασιν.
Θα ίδωμεν ότι οι νόμοι της Μηχανικής δεν ισχύουσι
ακριβώς ει μη εν τη τελευταία ταύτη περιπτώσει
θα είχομεν όμως μεγάλας δυσκολίας να τους εξερευνήσωμεν
εάν δεν ίσχυον κατά μεγάλην τουλάχιστον προσέγγισιν
και εις τας άλλας περιπτώσεις.
