832 - A quadratic corollary of Green-Tao Theorem
N. Lygeros
Theorem (Green-Tao) Let A be any subset of the prime numbers of positive relative upper density, thus
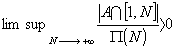
where 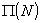 denotes the number of primes less than or equal to N. Then A contains arithmetic progressions of length K for all K.
denotes the number of primes less than or equal to N. Then A contains arithmetic progressions of length K for all K.
Specialization : Consider the set of primes p = 1 (mod 4)
Theorem : (classical) Every prime p = 1 (mod 4) can be written as the sum of two squares.
Quadratic corollary : There are arbitrarily long arithmetic progressions consisting of numbers which are the sum of two squares.
Special case : k = 4.
Theorem (Heath-Brown) Let S be the set of sums of two squares. There are infinitely many 4-term arithmetic progressions in S.
Proof : The numbers (n-1)2+(n-8)2, (n-7)2+(n+4)2, (n+7)2+(n-4)2 and (n+1)2+(n+8)2 form a 4-term arithmetic progression for any strictly positive integer.
Remark : n = 1 : 72, 62+52, 82+32, 22+92 (Degenerated cases)
n = 4 : 32+42, 32+82, 112, 52+122
n = 7 : 62+12, 112, 142+32, 82+152
n = 8 : 72, 12+122, 152+42, 92+172
