968 - Les arbres de Steiner ou des contraintes à la liberté
N. Lygeros
Classiquement les arbres de Steiner représentent la résolution d’un problème de minimisation. Celui-ci bien qu’il puisse être décrit élémentairement, est en réalité NP-complet. Néanmoins examinons d’abord la définition du problème initial. Dans le plan, nous nous donnons un ensemble fini de points distincts et nous désirons trouver un arbre de longueur minimale qui couvre l’ensemble de ces points. Si nous nous permettons de plus d’ajouter des points – points que nous nommons points de Steiner – alors la solution s’exprime sous la forme d’un arbre de Steiner. Considérons les exemples suivants pour mieux nous rendre compte de la complexité de cette simplicité.
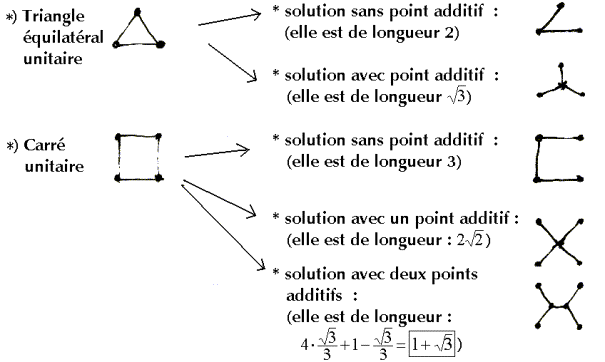
La construction détaillée de la dernière solution permet de comprendre l’exploitation du résultat obtenu à partir du triangle équilatéral.
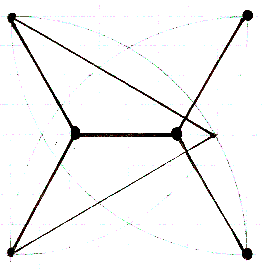 Il est à présent clair que le problème de la recherche d’un arbre minimal de Steiner revient à remplacer les contraintes sur la minimalité globale des arêtes par une liberté sur le choix des points additifs. La résolution du problème transforme les contraintes d’arêtes en liberté de points. Il y a déplacement de la difficulté opératoire par les règles de construction. Ainsi le problème devient un exercice qui appartient d’une part aux problèmes ouverts et d’autre part aux mathématiques cognitives. La liberté résout les Contraintes car c’est en cela qu’elle engendre un problème qui est difficile par sa simplicité et caractéristique de la cognition.
Il est à présent clair que le problème de la recherche d’un arbre minimal de Steiner revient à remplacer les contraintes sur la minimalité globale des arêtes par une liberté sur le choix des points additifs. La résolution du problème transforme les contraintes d’arêtes en liberté de points. Il y a déplacement de la difficulté opératoire par les règles de construction. Ainsi le problème devient un exercice qui appartient d’une part aux problèmes ouverts et d’autre part aux mathématiques cognitives. La liberté résout les Contraintes car c’est en cela qu’elle engendre un problème qui est difficile par sa simplicité et caractéristique de la cognition.
