1574 - Ταυτότητες του Newton και Αριθμοί του Fermat
Ν. Λυγερός
Όταν εξετάζουμε την παραγοντοποίηση έχουμε την τάση να θεωρούμε το άθροισμα των δυνάμεων ως πιο απλό σε σχέση με την αφαίρεση των δυνάμεων. Αυτό το φαινόμενο εξηγείται από την ύπαρξη ενός γενικού νοητικού σχήματος το οποίο θεωρεί ότι το άθροισμα είναι πιο απλό από την αφαίρεση. Αν και αυτό το σχήμα ισχύει όντως σε πολλούς χώρους, δεν εφαρμόζεται στο συγκεκριμένο πρόβλημα. Ο πρώτος λόγος είναι ότι το άθροισμα και η αφαίρεση είναι ισοδύναμα μέσα στο σώμα των μιγαδικών αριθμών. Το κυριότερο πρόβλημα όμως προέρχεται από τους πραγματικούς αριθμούς διότι δεν έχει λύση σε αυτό το σώμα κάθε πολυωνυμική εξίσωση. Ας εξετάσουμε λοιπόν, μετά από αυτήν τη διευκρίνιση, τις ταυτότητες του Newton σε σχέση με την παραγοντοποίηση.
Είναι γνωστό ότι: α3 + b3 = (α + b) (α2 – αb + b2). Και αυτή η ιδιότητα θεωρείται ως βασική εφόσον μέσω ενός απλού μετασχηματισμού επιτρέπει την εύρεση της εξής ταυτότητας: α3 – b3 = (α – b) (α2 + αb + b2). Στην πραγματικότητα, μέσα στο σώμα των πραγματικών αριθμών, η ουσιαστική ταυτότητα είναι η δεύτερη και όχι η πρώτη. Διότι η δεύτερη ανήκει σε μια γνωστή κλάση ως προς το θέμα της παραγοντοποίησης αn – bn. Η εξήγηση είναι απλή. Η εξίσωση αn – bn = 0 έχει πάντα τουλάχιστον μία ρίζα εφόσον αn – bn = 0 όταν α = b . Συνεπώς (α – b) | (αn – bn). Ενώ αυτή η ιδιότητα δεν ισχύει με την εξίσωση αn + bn. Πρέπει λοιπόν να ακολουθήσουμε μια άλλη στρατηγική στη διδακτική των μαθηματικών. Εξετάζουμε πρώτα την αφαίρεση που έχει μια γενική ιδιότητα για τις ταυτότητες του Newton και μετά το άθροισμα που αποτελείται από ειδικές περιπτώσεις.
- α2 – b2 = (α – b) (α + b), α3 – b3 = (α – b) (α2 + αb + b2), …
- Θεώρημα: α2 + b2 δεν έχει παραγοντοποίηση.
Απόδειξη : α = 2 b = 1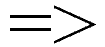 α2 + b2 = 5 πρώτος αριθμός συνεπώς δεν υπάρχει γενικός τύπος…
α2 + b2 = 5 πρώτος αριθμός συνεπώς δεν υπάρχει γενικός τύπος…
- Θεώρημα: α4 + b4 δεν έχει παραγοντοποίηση.
Απόδειξη Α: α = 2 b = 1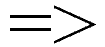 α4 + b4 = 17 πρώτος αριθμός συνεπώς δεν υπάρχει γενικός τύπος …
α4 + b4 = 17 πρώτος αριθμός συνεπώς δεν υπάρχει γενικός τύπος …
Απόδειξη B : α2 = Α και b2 = Β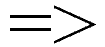 α4 + b4 = Α2 + Β2…
α4 + b4 = Α2 + Β2…
Ενώ α6 + b6 = (α2)3 + (b2)3 άρα εφαρμόζουμε την ταυτότητα α3 + b3 άρα υπάρχει παραγοντοποίηση.
Πιο γενικά, για κάθε N που διαρείται με περιττό αριθμό έχουμε παραγοντοποίηση.
Έστω N = M (2 n + 1) τότε αN + bN = (αM)2 n + 1 + (bM)2 n + 1 και εφαρμόζουμε την ταυτότητα του Newton α2 n + 1 + b2 n + 1 .
Συνεπώς μόνο οι αριθμοί της μορφής ![]() δεν έχουν γενική παραγοντοποίηση. Και είναι αυτή η ιδιότητα που εξηγεί την επιλογή της μορφής
δεν έχουν γενική παραγοντοποίηση. Και είναι αυτή η ιδιότητα που εξηγεί την επιλογή της μορφής ![]() για τους αριθμούς του Fermat που αποτελούν μια ειδική περίπτωση (α = 2, b = 1) δίχως αυτό να σημαίνει ότι είναι πάντα πρώτοι (641 |
για τους αριθμούς του Fermat που αποτελούν μια ειδική περίπτωση (α = 2, b = 1) δίχως αυτό να σημαίνει ότι είναι πάντα πρώτοι (641 | ![]() Euler).
Euler).
