Un des premiers domaines à étudier dans le cadre de la théorie des jeux, c’est celui des duopoles. En effet, il représente le cas le plus simple qui ne soit pas dégénéré comme celui de monopole et qui permette de mettre en évidence l’interaction des joueurs. De plus, il offre la possibilité d’étudier les modèles de cette interaction et de montrer qu’il n’existe pas de hiérarchie
totalement ordonnée.

Le premier modèle de duopole, c’est celui de Cournot. Dans ce modèle, nous avons deux entreprises qui produisent un produit homogène à des niveaux y₁ et y₂ qui peuvent être agrégés en Y = y₁ + y₂. Le prix du marché associé à la fonction de demande inverse correspond à p(Y) =
p(y₁ + y₂) et la fonction coût de chaque
entreprise est c₁(y₁) et c₂(y₂). Ainsi la maximisation de la première entreprise est : . Comme ce profit dépend du niveau de l’autre entreprise et vice versa, cela revient pour chaque joueur à prévoir le coup de l’autre. Il s’agit donc d’un jeu, au sens de la théorie, en une étape. Sa résolution exploite la notion de courbes de réaction dont l’intersection représente un équilibre de Nash. Il est néanmoins possible de l’interpréter comme une convergence qui se stabilise sur un équilibre dont la stabilité dépend des courbes de réaction.

La différence qu’introduit le modèle de Bertrand, c’est qu’au lieu de considérer comme espace stratégique la quantité, nous nous intéressons au prix. Si D(p) est la courbe de la demande du marché et c₁ et c₂ les coûts des entreprises. La courbe de demande de la
première entreprise est : 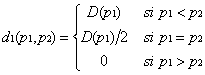. L’équilibre de Nash est obtenu en posant p₁ = c₂ et en produisant D(c₂) tandis que la seconde fixe et ne produit rien. Bien sûr cela peut sembler quelque peu irréaliste. Cela s’explique par le fait que le jeu s’effectue en une étape.

Le modèle de Stackelberg introduit une nouvelle différence qui consiste à faire
jouer l’entreprise leader en premier et après l’analyse de ce choix, l’entreprise qui suit peut optimiser son choix. Cette fois, nous avons un jeu à
deux étapes. Et le point d’équilibre est obtenu quand une courbe de réaction est tangente aux lignes d’isoprofit de l’autre. Nous pouvons en déduire que l’équilibre de Stackelberg est meilleur que l’équilibre de Cournot puisqu’il a
le choix du point optimal. Cela implique aussi que dans le cas idéal, il est
préférable d’être leader. Ces résultats sont évidemment compatibles avec la théorie de l’information.

Un modèle quelque peu semblable consiste à considérer comme donné le prix fixé
par la première, il s’agit du price leadership. Il se résout de la même manière
que le modèle de Stackelberg. Via ces modèles qui appartiennent tous au cadre
non coopératif, nous pouvons explicitement voir à quel point le choix des règles
influence les points d’équilibres qui ne peuvent se comparer que dans des
circonstances particulières, fait qui est fondamental si nous désirons comprendre les stratégies plus complexes qui utilisent plusieurs étapes.