A partir de la théorie des groupes de Galois, nous pouvons généraliser la notion d’élément neutre via la méthodologie de Frédéric Marty qui met en évidence l’axiome de reproduction et en lui rajoutant l’associativité, nous pouvons construire l’ensemble de ce que nous appelons désormais les hypergroupes de Marty. Nous remarquons donc que dans cette généralisation l’associativité n’est pas affectée. Aussi il est naturel, a posteriori de la généraliser aussi comme l’a, entre autres, fait Vougiouklis afin de créer les Hv-groupes et par la suite les Hv-structures, en remplaçant l’égalité par une intersection non nulle. Pourtant cette voie même si elle conduit à de nombreux résultats, n’est pas nécessairement universelle.

En effet si nous considérons la construction de Cayley-Dickson ou celle de Conway-Smith qui permettent d’engendrer via les complexes, l’ensemble des quaternions d’Hamilton, l’ensemble des octonions de Cayley, etc. alors l’associativité devient une opération plus importante en raison de sa disparition dans l’ensemble des octonions. Dans ce cadre, il est naturel a posteriori de la remplacer par l’identité de Ruth Moufang et non seulement se contenter de l’affaiblir à l’aide d’une opération ensembliste.

Aussi de manière analogue à la création des hypergroupes de Marty, nous pouvons construire les hypergroupes de Moufang qui vérifient donc deux axiomes à savoir celui de la neutralité et celui de l’identité de Moufang. Par définition, les hypergroupes de Moufang comme les hypergroupes de Marty généralisent les groupes de Galois. Cependant les hypergroupes de Moufang s’ils vérifiaient l’axiome de reproduction généraliseraient aussi ceux de Marty puisque ces derniers y sont inclus. Cela est évident en raison de la construction puisque l’identité de Moufang est plus faible que celle de l’associativité. Par contre elle demeure une égalité au sens classique du terme.

Cette seconde généralisation i.e. du second axiome seulement, permet de compléter naturellement celle du premier, effectuée par Marty. Ainsi à partir des groupes de Galois nous avons d’une part une généralisation de Marty – axiome de reproduction – et d’autre part une généralisation de Moufang – identité de Moufang. Nous appelons cette structure : hypergroupe de Marty-Moufang.

Ainsi nous pouvons mettre en évidence les structures suivantes :
– Groupe de Galois
– Hypergroupe de Marty (Axiome de Reproduction + Associativité)
– Hypergroupe de Moufang (Neutralité + Identité)
– Hypergroupe de Marty-Moufang (Axiome de Reproduction + Identité)

Et les relations ensemblistes suivantes :

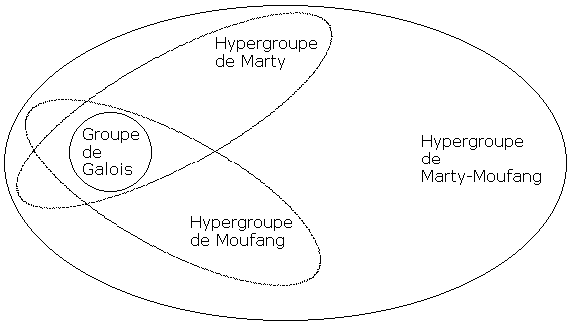
De cette manière nous avons une vision plus globale de la généralisation dans cette théorie.