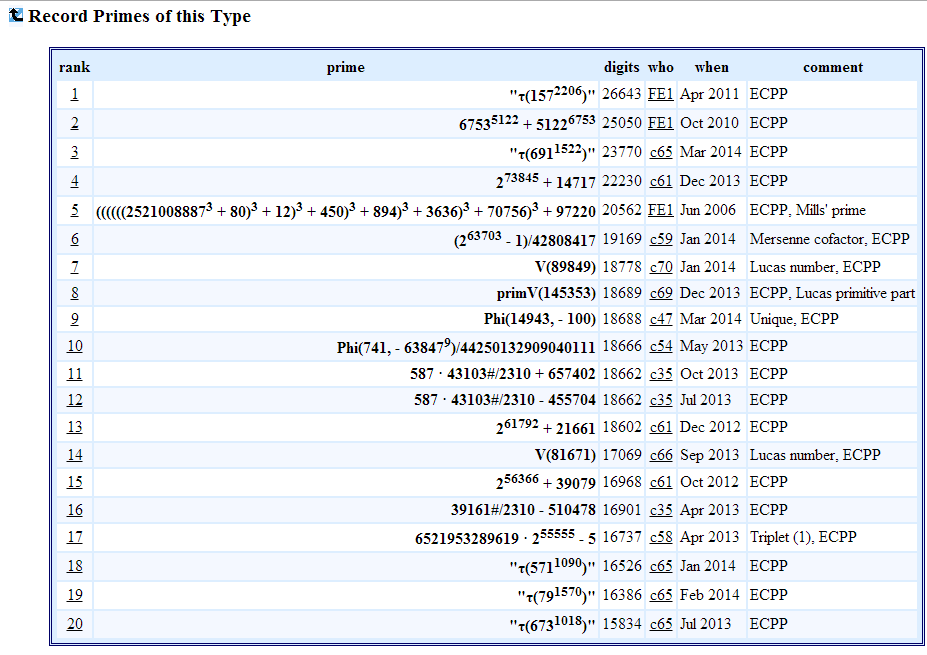
Αν εξετάσουμε τον πίνακα της παγκόσμιας κατάταξης των πρώτων αριθμών που έχουν πιστοποιηθεί αποκλειστικά με τη μέθοδο των ελλειπτικών καμπυλών, μπορούμε να δούμε ότι υπάρχουν διάφοροι τύποι. Αυτοί δεν είναι κλασικοί και συμβατικοί και η πιστοποίηση τους απαιτεί ένα γενικό πρόγραμμα, τουλάχιστον προς το παρόν, για να υλοποιηθεί. Υπάρχει βέβαια ένα σκέλος από αριθμό Mersenne, ένας πρώτος που προέρχεται από αριθμό Lucas, δύο αριθμοί Lucas, δύο αριθμοί που σχετίζονται με τη συνάρτηση Φ, αριθμοί που αποτελούνται από άθροισμα δυνάμεων, δύο συνδυασμοί από πρώτο παραγοντικό κι ένας πρώτος του Mills. Βλέπουμε ότι το φάσμα είναι ευρύ. Σε αυτό το πλαίσιο εντάσσεται και η έρευνά μας πάνω στους αριθμούς Lehmer-Ramanujan που κατασκευάζονται μέσω της συνάρτησης τ του Ramanujan, γενικεύοντας την ιδιόμορφη προσέγγιση του Lehmer. Με αυτόν τον τρόπο καταφέραμε να εντάξουμε πέντε πρώτους αριθμούς LR στην κατάταξη που αποτελείται σε παγκόσμιο επίπεδο από είκοσι πρώτους αριθμούς. Έτσι οι αριθμοί τ(157²²⁰⁶ ), τ(691 ¹⁵²²), τ(571¹⁰⁹⁰), τ(79¹⁵⁷⁰) και τ(673¹⁰¹⁸) κατέχουν τις θέσεις 1,3,18,19 και 20. Με άλλα λόγια υλοποιούν το όραμα του άρθρου μας με τίτλο: Odd prime values of the Ramanujan tau function, που δημοσιεύσαμε στο The Ramanujan Journal στις 15/03/2013. Αφού δείχνουν επί του πρακτέου την αποτελεσματικότητα της μεθοδολογίας μας για την εύρεση μεγάλων πρώτων αριθμών.