151 - The Eureka Test
N. Lygeros
Perfection 1 01/2000, Gift of Fire 112, 01/2000, In-Genius 161, 02/2000, Thoth 20, 2/2000, Noesis 147, 4/2000.
N. Lygeros
14 avenue Condorcet, 69100 Villeurbanne, France.
Brainpower and serendipity are needed for this test designed for visual-spatial and mathematically gifted.
Please supply the following information:
Test : Eureka Test
Name :
Address :
Highest educational level attained :
Age and sex :
Previous test-scores including the names of the tests and the dates :
High-IQ society memberships :
Solutions with explanations :
FEES : 6 neurons or 10 euros or 12 $.
REMARKS : No time limit, no discussions with others.
The Eureka test is an admission test for Sigma and Mega Foundation
The pictures 1,2,3,4,5,6,7,8,10 have been created by Ph. Jacqueroux and 9 by M.C. Escher.
CHANGES :
01/03/2000 : modification of the english translation (Thanks to S. Schuessler and B. Seitz)
01/28/2000 : item 6 : more precise formulation (Thanks to K. Langdon)
01/30/2000 : item 9 : more precise formulation (Thanks to Ch. Currivan and K. Langdon)
02/15/2000 : translation in spanish by J. Martinez
02/15/2000 : translation in german by Th. Riepe
1) Find the number of non-attacking queens necessary to cover a toroidal chess-board of 64 squares and prove that this number is minimal.

2) Find the necessary and sufficient number of vertices for a graph to be non-representable on the surface of the torus without any of its edges crossing. Build such a graph.
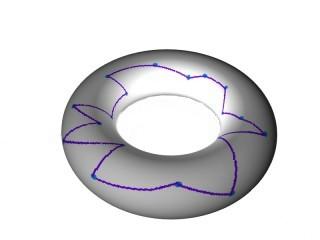
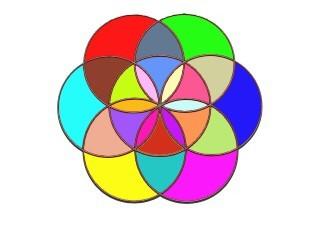
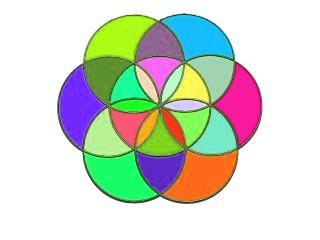
3) By numbering the areas from 1 to 24, build two magic rosettes the sum of whose areas (for each of their discs) is equal to 80 and to 84 respectively.
4) Find the necessary and sufficient number of identical cubes joined together, with adjacent cubes joined only through the superposition of one whole face of one on one whole face of another, to build a trefoil knot in three dimensions.

5) Construct all possible non-isomorphic configurations with a tetrahedron, an octahedron and an icosahedron (two objects have a common face or an empty intersection).

6) With L , build 9 non-isomorphic cellular tori of height and depth 3 and thickness 1.

7) What is the volume of the smallest possible cube containing 9 unit cubes?

8) Construct a minimal terminal dendromino with tetrahedrons.
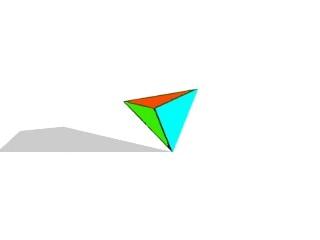
9) Find the number of non-isomorphic geometric objects obtained by cutting out a Möbius strip while remaining parallel on its board and describe them.
10) Find the necessary and sufficient number of non-attacking queens to cover a cubic chess-board of 64 boxes.