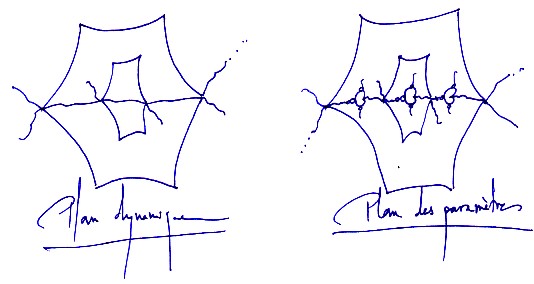
1700 - Modèle de Thurston et Puzzles de Yoccoz
N. Lygeros
Dans le cadre des travaux de Douady et Hubbard, notre connaissance des propriétés dynamiques de la famille des polynômes quadratiques complexes, peut être synthétisée par l’ensemble de Mandelbrot qui représente un dictionnaire des ensembles de Julia. L’ensemble de Mandelbrot peut lui-même être appréhendé de manière efficace grâce au modèle abstrait de Thurston, qui est obtenu par le pincement multiple du disque. Seulement pour démontrer que le modèle est véritablement homéomorphe à l’ensemble de Mandelbrot, il est nécessaire de prouver que ce dernier est localement connexe. La connexité de cet ensemble avait été démontrée par Douady et Hubbard. Un des résultats les plus importants dans le cadre de la conjecture MLC, c’est celui de Yoccoz qui a montré que l’ensemble de Mandelbrot est localement connexe en tout point non infiniment renormalisable i.e. non contenu dans l’intersection d’une suite décroissante de copies de l’ensemble. Dans le cas des points qui ne se trouvent pas sur le bord d’une composante hyperbolique (i.e. sous ensemble dont le centre est un point périodique), Yoccoz s’est attaché à la cardioïde principale et aux membres qui la touchent aux points d’argument interne rationnel. Il a tout d’abord montré que le diamètre d’un membre attaché au point d’argument interne p/q est majoré par une formule du type c/q où c est une constante. Et ensuite il a généralisé cette méthode à toute composante hyperbolique de l’ensemble de Mandelbrot. Par contre, pour les points qui ne sont ni infiniment renormalisables, Yoccoz a employé la méthode des puzzles. En prenant comme point de départ le travail de Branner et Hubbard sur une famille de polynômes cubiques. En exploitant l’inégalité de Grötzsch, il suffit de montrer qu’une suite d’anneaux emboîtés dont la somme des modules est infinie contient l’ensemble qui doit aboutir à un point. Une fois le résultat obtenu dans le plan dynamique, il faut le transférer dans celui des paramètres. Seulement dans le cas de l’ensemble de Mandelbrot, le transfert est un véritable tour de force. Pour ce faire, Yoccoz a introduit les puzzles. La pièce du puzzle est limitée par des rayons externes et des arcs d’équipotentielles. Comme une telle pièce découpe un ensemble connexe dans l’ensemble de Mandelbrot, la démonstration de la conjecture MLC en un point est obtenue en montrant que l’intersection des pièces qui sont des voisinages de c est réduite à c. La difficulté provient de l’absence de correspondance conforme à l’intérieur des ensembles considérés. Le plus caractéristique de cette absence, c’est la présence d’une infinité de copies de l’ensemble de Mandelbrot dans le plan des paramètres. Aussi les anneaux n’ont pas même module et il est extrêmement difficile de montrer que le rapport des modules est borné. Cependant grâce à ses puzzles, Yoccoz est parvenu à surmonter cette difficulté. Ainsi après ces résultats, la démonstration de la conjecture MLC se ramène à celle des points infiniment renormalisables. Ce type de résultat est caractéristique de la capacité de la géométrie à visualiser de manière élégante des problèmes d’analyse fine qui ne peuvent être résolus de manière brutale et directe. Il est donc analogue au schéma mental que nous avons présenté dans notre article intitulé Proposition visuelle mais cette fois dans le domaine de l’analyse.