Όπως το επισημάναμε σ’ ένα προηγούμενο άρθρο (βλέπε opus 1595), στο βιβλίο 50 επιστολές… υπάρχει η σημείωση 47 που εξηγεί ότι η διάτρηση του χαρτιού δεν επιτρέπει την ανάγνωση ενός τύπου της επιστολής Carathéodory προς Hilbert (βλέπε Cod. Ms. D.Hilbert 55,5). Στο άρθρο μας, μέσω μαθηματικών υπολογισμών συμπεράναμε ότι ο ολοκληρωμένος τύπος είναι : |f(x)|< M_n.

Τώρα, μετά την αποστολή μας στο Göttingen μέσω του Υπουργείου Εξωτερικών Ελλάδας, μπορούμε να αποδείξουμε τον προηγούμενο ισχυρισμό μας. Όντως η προσεχτική εξέταση του πρωτότυπου της επιστολής στα αρχεία της βιβλιοθήκης μάς επιτρέπει να αναδείξουμε μερικά καθοριστικά στοιχεία.

Η διάτρηση του χαρτιού προέρχεται από την κλασική αρχειοθέτηση των επιστολών που ευτυχώς δεν χρησιμοποιείται πια διότι καταστρέφει μερικώς το χειρογράφο. Η συγκεκριμένη διάτρηση έχει το συμβατικό μέγεθος της διπλής διάτρησης ενός φακελώματος. Συνεπώς δεν μπορεί να έκρυβε πολλά σύμβολα. Επιπλέον η σημείωση του Carathéodory που ακολουθεί τον ελλιπή τύπο, μας αναγκάζει να υποθέσουμε ότι υπήρχε το σχήμα Mn. Άρα το θέμα είναι αν υπήρχαν επιπλέον διακριτικά στοιχεία. Αυτή η απορία μπορεί να λυθεί με τον συνδυασμό της χρήσης ενός μεγεθυντικού φακού και της ανάλυσης του γραφικού χαρακτήρα του Carathéodory.

Ο Carathéodory, όπως το δείχνουν οι χειρόγραφες επιστολές του, χρησιμοποιούσε πένα και μάλιστα κονδυλοφόρο σε μερικές περιπτώσεις. Δεν είχε λοιπόν την ελευθερία της καμπυλότητας που επιτρέπει το σημερινό στυλό. Ο Carathéodory σπούδασε πρώτα στο Βέλγιο με το γαλλικό σύστημα κι ύστερα στη Γερμανία. Και ο γραφικός του χαρακτήρας είναι επηρεασμένος από τον τρόπο γραφής των λατινικών γραμμάτων που χρησιμοποιούν αυτές οι χώρες, ειδικά όταν γράφει στα γερμανικά. Το κεφαλαίο M του Carathéodory έχει τις εξής ιδιότητες: -είναι καθαρά ασύμμετρο ως προς τα πόδια του -είναι μείγμα γραμμικότητας και καμπυλότητας. Το αριστερό πόδι έχει ένα γραμμικό σπάσιμο. Ξεκινά με μία μικρή διαγώνιο και συνεχίζει κάθετα προς τα πάνω μετά από μια κλειστή γωνία. Το δεξί πόδι καταλήγει μετά από κάθετο σε μια πολύ κυρτή καμπυλότητα που κλείνει εσωτερικά με μια στροφή προς τα αριστερά. Άρα το δεξί πόδι δεν κατεβαίνει πιο κάτω από το αριστερό. Και όταν ο Carathéodory βάζει ένα δείκτη σ’ ένα γράμμα χρησιμοποιεί μια πολύ μικρή απόσταση. Όταν πρόκειται για (n) μικρό, έχουμε και πάλι μια πολύ μικρή γωνία στο αριστερό πόδι και στο δεξί μια καμπυλότητα που εφάπτεται του οριζόντιου άξονα της γραφής. Ο φακός δείχνει ξεκάθαρα στο κάτω μέρος της διάτρησης τη διαγώνιο και τη γωνία του αριστερού ποδιού του (Μ) και τη μικρή γωνία του αριστερού ποδιού του (n) και επίσης τη διπλή καμπυλότητα με εφαπτόμενη του δεξιού ποδιού.

Ως αποτέλεσμα αυτής της ειδικής μελέτης της επιστολής του Carathéodory προς Hilbert που αφορά τη χρήση της μεθοδολογίας του Fourier, έχουμε τον εξής ολοκληρωμένο τύπο: |f(x)|< M_n όπου 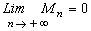πράγμα το οποίο συμπληρώνει τα μαθηματικά μας συμπεράσματα. Κατά συνέπεια αυτή η ολοκλήρωση αποδεικνύει έμμεσα και την αναγκαιότητα της πρόσβασης στα χειρόγραφα.