20699 - Βασικές καταστροφές και θεμελιακές σκέψεις
Ν. Λυγερός
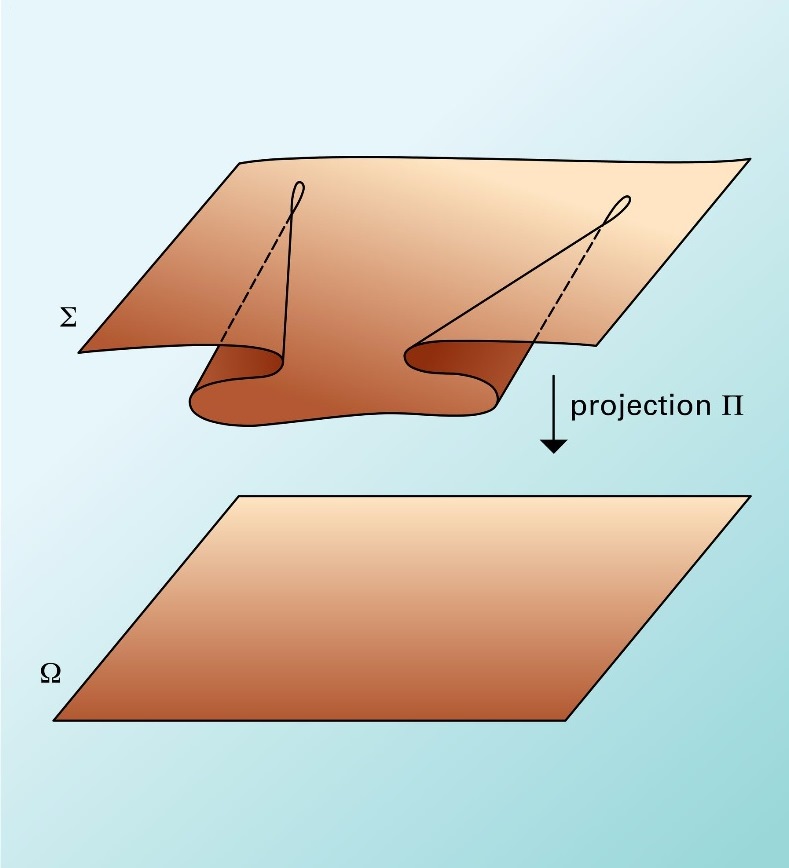
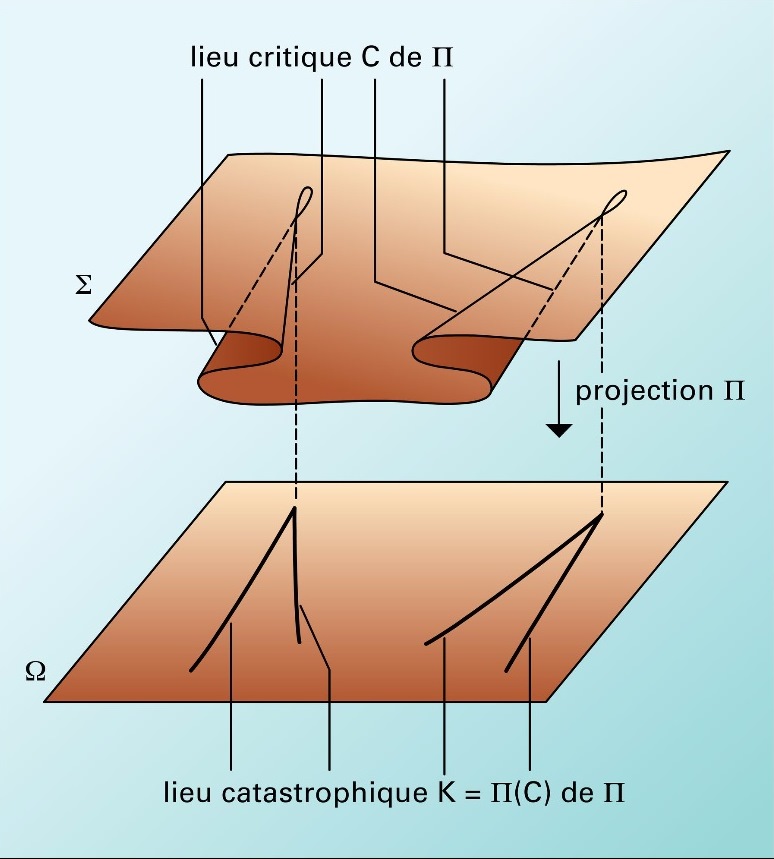
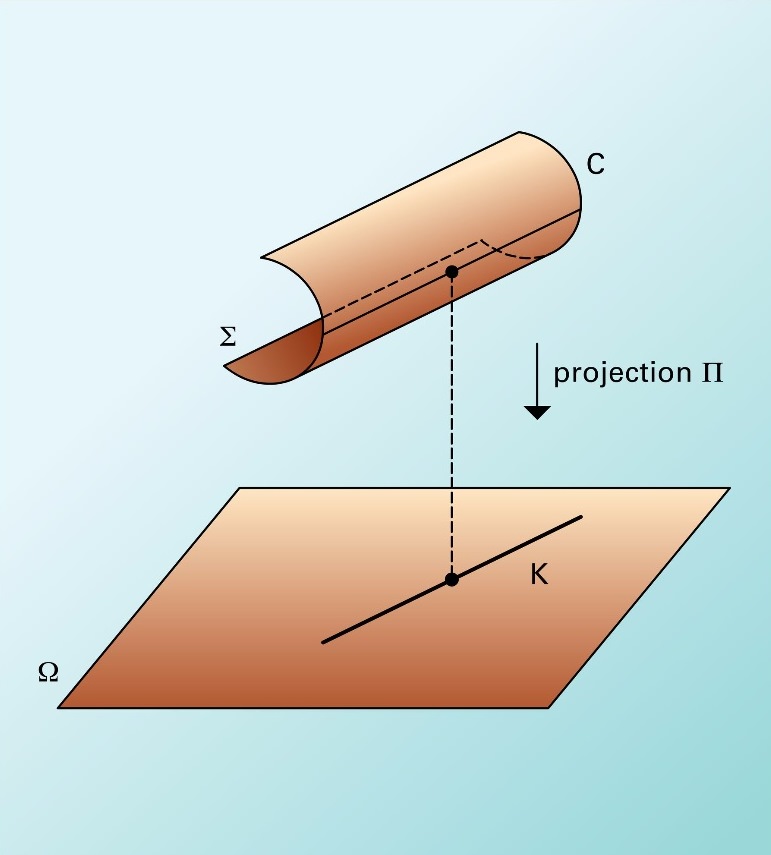
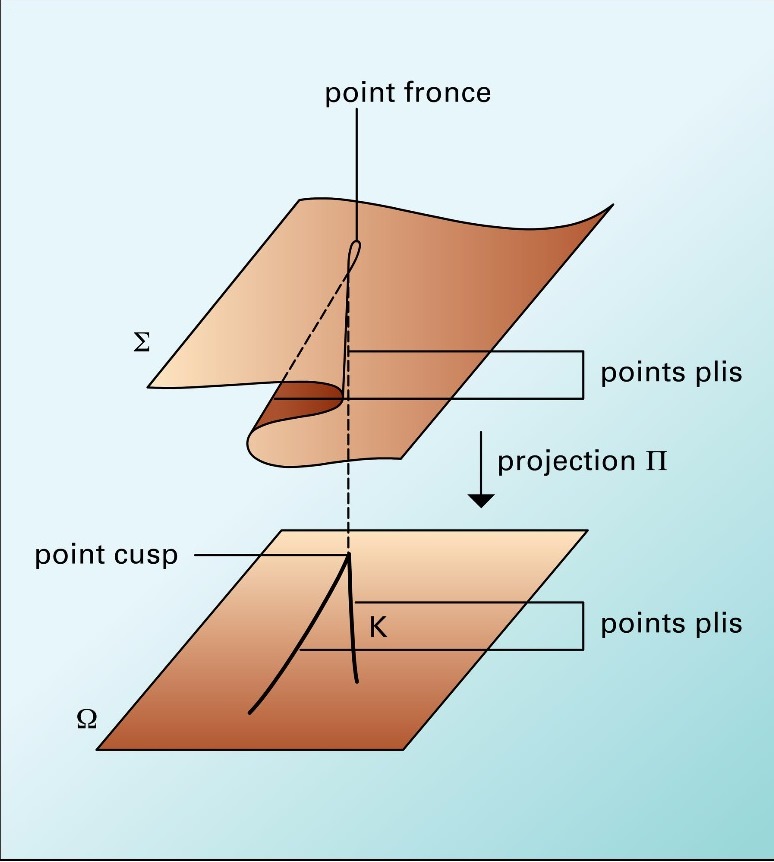
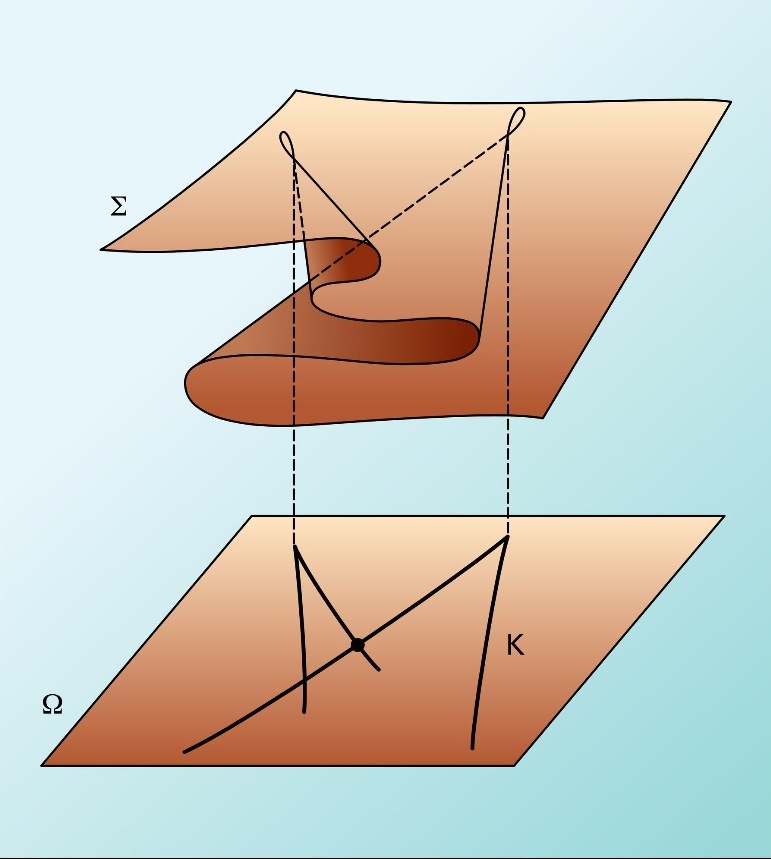
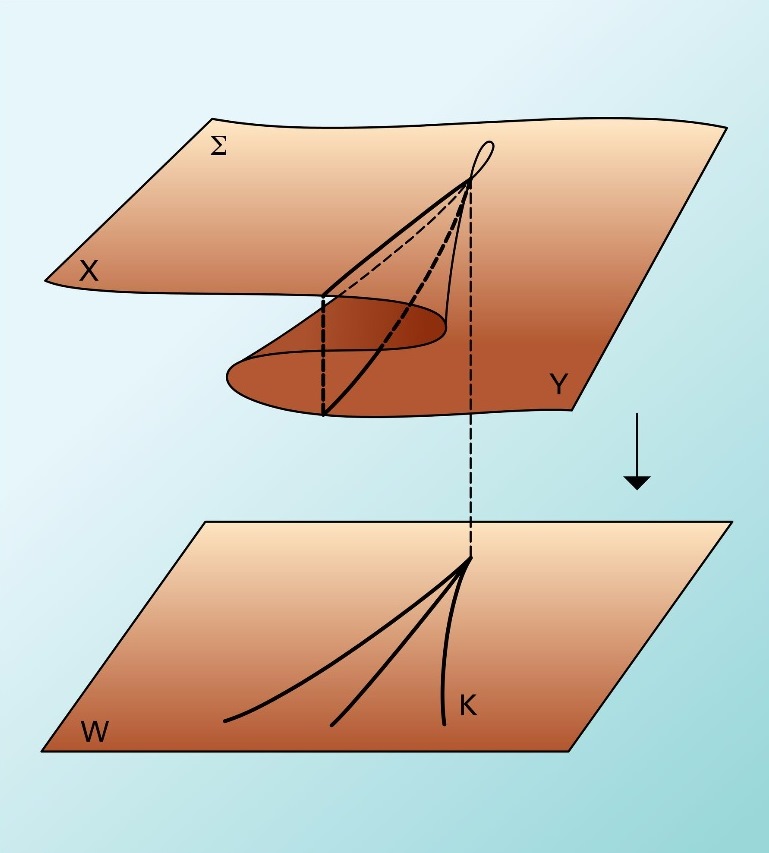
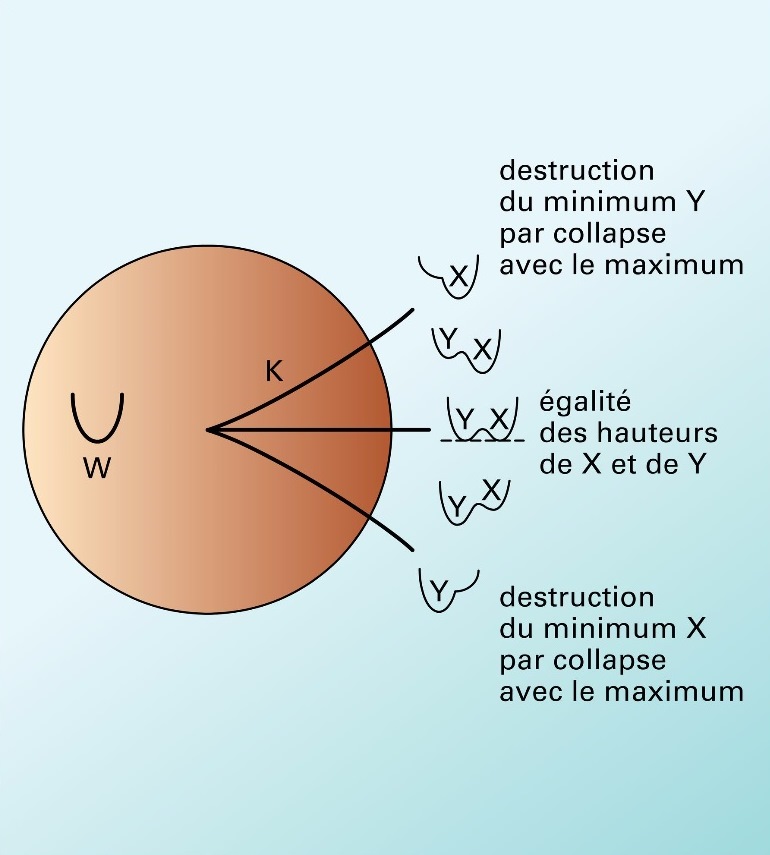
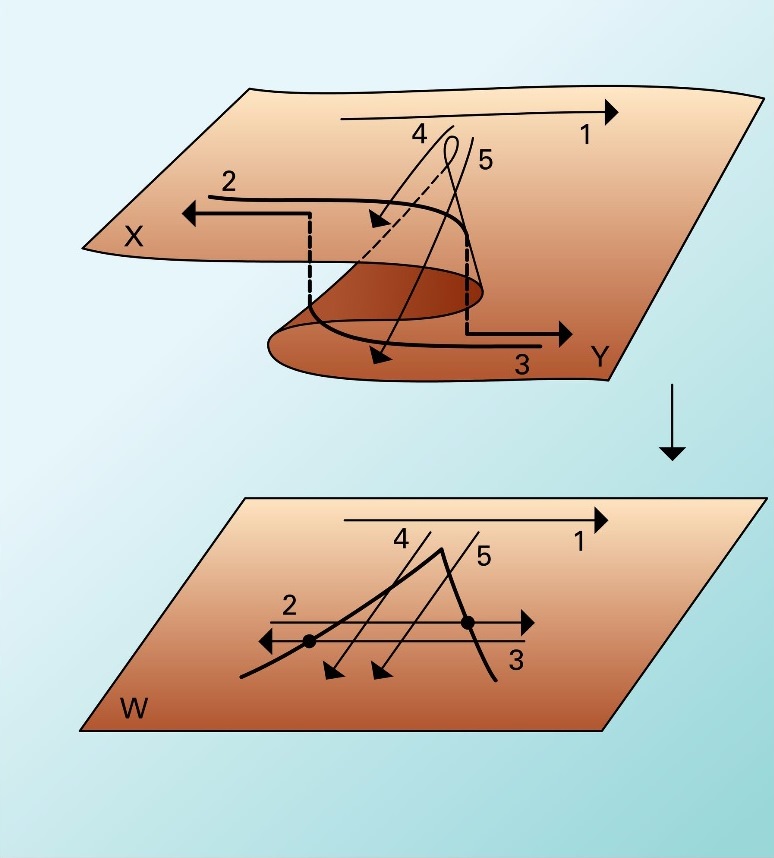
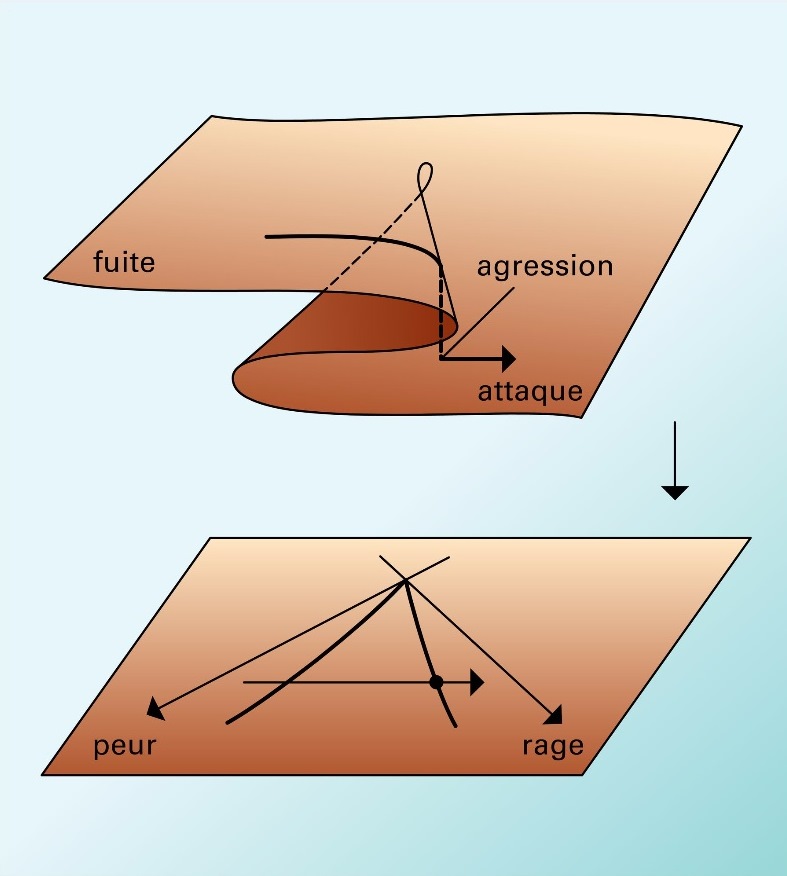
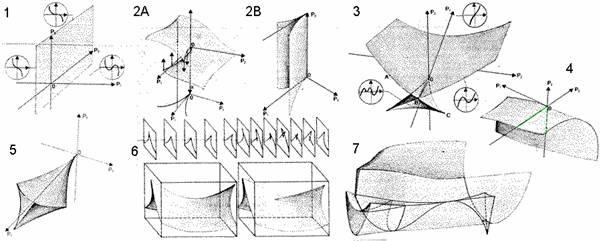
Με τη θεωρία καταστροφών, ο R. Thom κατάφερε να ταξινομήσει τις καταστροφές σε συνάρτηση με το πλήθος των παραμέτρων εισόδου, το πλήθος των άγνωστων εξόδου και την τιμή του δυναμικού του συστήματος.
Για a και x έχουμε: V= x3+ax
Για (a,b) και x έχουμε: V= x4+ax2+bx
Για (a,b,c) και x έχουμε: V=x5+ax3+bx2+cx
Για (a,b,c) και (x,y) έχουμε: V=x3+y3+axy+bx+cy
ή V=x3/3-xy2+a(x2+y2)+bc+y
Για (a,b,c,d) και x έχουμε: V=x6+ax4+bx3+cx2+dx
Για (a,b,c,d) και (x,y) έχουμε: V= x2y+y4+ax2+by2+cx+dy
Με αυτά τα δεδομένα μπορούμε να αξιοποιήσουμε και την ταξινόμηση ADE του Arnold μέσω των απλών ομάδων Lie. Αυτό σημαίνει πρακτικά ότι κάποιος που γνωρίζει αυτά τα νοητικά σχήματα θα λειτουργήσει διαφορετικά σε μια διαπραγμάτευση και θα εκμεταλλευτεί τις καταστροφές ανάλογα με τις παραμέτρους εισόδου, για να προβλέψει τη συνέχεια ακόμα κι όταν υπάρχουν φαινόμενα ασυνέχειας. Πρακτικά, κάποιος που δεν κατέχει το αντικείμενο όσα σχέδια και να έχει, θα πετύχει μια ισορροπία μόνο και μόνο αν το θέλει ο άλλος, αλλιώς βρίσκεται στην αδιέξοδο της διακλάδωσης.