50962 - Complexity and organisation in biological and intelligent systems
Marco Piumetti, Nik Lygeros
KEYWORDS
complex systems biology; self-organizing phenomena; biochemistry; collective intelligence; mankind.
ABSTRACT
Biological systems exhibit emerging collective behaviors thanks to non-linear interactions among the components. The creation of self-organizing phenomena tends to spontaneously organize the systems structurally, thus becoming progressively more ordered and differentiated. Furthermore, biological systems, from bacteria colonies to more highly evolved organisms, exhibit a form of collective and organized intelligence, a type of distributed intelligence that is present since the beginning of Life on Earth.
- Introduction
Living organisms are made up of biological structures, cells, that are able to carry out the functions of living things, such as being born, feeding, growing, reproduction and finally dying but able to give live again even after their death. Each cell has a well-defined internal organisation in which the parts interact within a dynamic system. This means that an organism is not just made up of many parts, but the latter communicate to each other in a highly intricate manner and are different in form and function that’s why we need a systemic approach or even a holistic one for irreducible complexity.
Simple organisms consist in single cells such as bacteria, protozoa and some algae and yeast. Bacteria, one of the simplest forms of life imaginable, have a cell wall made of peptidoglycan, under which lies the cell membrane. This is an important biological structure that contains enzymes able to carry on the metabolic processes at relatively low temperatures. On the other hand, pluricellular organisms (namely, plants, animals and many fungi) are made up of many cells able to interact with each other thus maintaining the physiological equilibrium in the whole organism, but this communication needs a subtract i.e. a connection system for the transmission of necessary information [1].
The human being, for instance, the most complex living organism on Earth, is made up of approximately a hundred billion cells, all different from a morphological and functional point of view. The various cells are organised into tissues, which form the organs. The latter may form apparatus/systems and these in turn work together to make up the living organism. This is the starting point of the notion of hierarchy in the framework of comparisons and complementarity.
These biological systems are hierarchical and also modular in the sense that certain structures and functions underlay others but also are rather autonomous even if they belong to the same structure, so we get both local and global aspects in this kind of system and we need different scales of study. Intercellular communication coordinates activities between cells making various physiological processes possible, such as the immune response, growth and homeostasis. Conversely, a lack of correct communication among cells can lead to the development of several diseases, including some types of cancer [2].
In this scenario, a global view integrating structure, dynamics, control and design become necessary to cope with them and with similar issues arising in a host of other conditions because the simple analysis of them is insufficient to understand their life. In the present work, we outline the main ideas that are being developed in complex systems biology and comment on open questions and future perspectives.
- Non-linearity and self-organization
A living organism is an open system subjected to non-equilibrium conditions in which the variables depend on biochemical reactions and transport phenomena. Such reaction-diffusion systems can be mathematically described by the semi-linear parabolic partial differential equations:
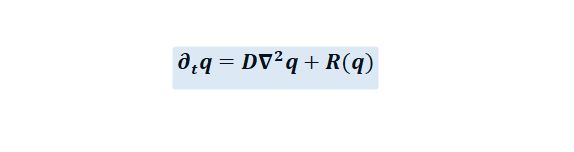
where q (x, t) denotes the vector function, D is a diagonal matrix of diffusion coefficients and R accounts for all local reactions. The solutions of reaction–diffusion equations lead to the formation of self-organized patterns and this is a way to create fractal objects. Biological systems, in fact, tend to spontaneously organise themselves in more and more organised, differentiated and complex structures which means that locally they minimize entropy. Spontaneous folding of proteins and other bio-macromolecules, formation of lipid bilayer membranes as well as morphogenesis are all examples of self-organization.
Self-organized patterns, including the Turing [3] and Wiener systems [4], typically appear as a consequence of three main components: strong dynamical non-linearity, balance of exploitation and exploration and multiple interactions.
A specific case of such nonlinear behavior occurs in self-sustained oscillations. These phenomena arise at various scales, from molecular to supercellular structures, with periods ranging from seconds (e.g. membrane potential oscillations, cardiac rhythms, calcium oscillations, etc.) to hours (e.g.
cell cycle, circadian rhythms, etc.) or even days (e.g. metamorphosis systems).
At subcellular level, a characteristic example of non-linearity (oscillatory behavior) can be observed with certain enzymes. Specifically, periodicity in enzymatic reactions seems due to the following causes: It can result from periodicity in enzyme synthesis owing to control mechanisms at the genetic or translation levels (epigenetic oscillations) or to periodicity in enzyme activity owing to regulation at the level of the enzyme itself (metabolic oscillations) [5].
Thus, a variety of regulatory enzymes that participate in various metabolic reactions may induce the nonlinearities in the cellular metabolism and totally change its behaviour at different scales [6,7].
- Emerging collective structures
Living organisms usually show emerging collective structures because of the interaction among the biological structures, e.g. proteins, DNA, nuclei, cells, tissues, organs, etc. [5,6]. A collective structure emerges from the sum of the elements. Thus, an organism is superior and more complex to the sum of its parts because the combinatorial part is not independent. Different biological structures are able to interact with each other to carry out the vital functions of a living organism, that alone they would be unable to achieve, thus generating a complex system with a hierarchical, multi-scale organisation. Each sub-system offers its own contribution to the final whole being in a complementary manner. The intrinsic order of a living organism is significantly higher than that of a crystalline structure. In this “almost perfect” structural order the enzymes, the biological catalysts par excellence, allow metabolic reactions to take place at temperatures compatible with life systems. Without enzymes, life as we know it would not be possible. Similarly, the shape and behaviour of a bacterial colony or a flock of birds or a school of fish are examples of emerging collective structures which can be examined with game theory in mathematics [8,9]. An application of game theory to evolving populations in biology was already introduced by J. Maynard Smith in 1973 [10].
From these biological systems arise macroscopic properties that are difficult to predict by the laws that govern the single components because we have to study also the relations between scales. However, it is not only the number of relationships among single components that favour the appearance of emerging non-linear behaviour, but also their organization. Such biological systems that interact and evolve over time can be described using mathematical laws and physical characteristic specifications, as they must maintain conditions of dynamic equilibrium.
A biological system has its own specific laws that derive from the non-linear interaction of a number of components and that make up a unique dynamic entity that is organised and capable of adapting to the environment [11,12]. Already in 1911 Wheeler observed how apparently independent organisms are able to work together so closely that they became indistinguishable from a single organism. He called this a “super-organism” [13]. This biological superstructure, which can be interpreted as a hyperstructure in mathematics [14,15], is more complex than a structure, exhibits adaptive properties, namely to be reactive and flexible over time. In fact, biological systems transcend the level of the single organisms and create large scale structures and functions which are impossible at the previous level. Thus, the new scale has more degrees of freedom. For instance, cells in vitro spontaneously form assemblies with coordinated social behavior and creation of ordered morphological patterns [16].
This suggests that different organism groups, from bacteria colonies to tribes, have a form of delocalized organisation and collective intelligence, effective to adapt and adjust the system to environmental conditions. This super-structure is fundamental for biological systems since it is polymorphous and even but also protean and typically acts via the heuristic approach. Thus, biological systems accumulate progressive changes over time and in turn is pivotal for the evolutionary processes. Studies of collective intelligence in animal groups, indeed, confirmed that the latter can accumulate progressive modifications over time even at very large scale [17]. This means that we have a change of phase or even a cycle which leads to the notion of polycyclicity in mathematics.
- Life from physical point of view
As a whole, the laws of physics and chemistry are inaccurate with a relative error of the order of 1/√n where n represents the number of elements involved. This is due to the effect of the combination of those elements. The laws are able to explain processes at this level but not at different domains at the same time. The physiological activity of living organisms must obey to the laws of physics. This means that a living organism must have a very high number of components (molecules, ions…) in order to benefit from through laws that guarantee its survival [18].
Life depends on an orderly pattern and follows the physical laws, not exclusively based on the tendency to proceed from order to disorder but on the conservation of the existing order. This is possible, from a thermodynamic point of view, as living organisms are open systems that exchange energy and matter with the environment [18]. For instance, the order created within the cells is more than compensated by the disorder produced in their environment.
Since biological processes take place at roughly constant temperature and pressure, the Gibbs free energy (ΔG = ΔH – TΔS) can be a useful way to express the second law of thermodynamics. The minimization of the ΔG is a form of the principle of minimum energy, with follows from the entropy maximization principle for closed systems. In other words, living organisms preserve their internal order by taking from their surroundings free energy (i.e. in the form of nutrients or sunlight) and returning to their surroundings an equal amount of energy as heat and entropy. Furthermore, living organisms are dissipative structures, namely thermodynamically open systems, that work in a state far from the thermodynamic equilibrium exchanging energy, matter and/or entropy with the environment. The latter systems are characterised by the spontaneous formation of anisotropy, ordered and complex structures [19] which can be interpreted as a result of some points of Ramsey theory. This point is also in relation with the evolution of mankind as a collective and organised high level intelligence.
- Action by chance and of necessity
In 1970 Jacques Monod introduced the concept of teleonomy that sees the in situ finality of living things as a result of natural selection [20]. Monod thought that one of the fundamental properties of all living organisms was to have a project, teleonomy, represented by their structure and put into action by their performance. Such a project consists of the conservation and preservation of the species, by passing on genetic information from one generation to another. Each teleonomic structure represents a given quantity of information that is transmitted to another structure in an identical way. This characteristic, which is essential to organisms, is known as invariant reproduction or reproductive invariance. Reproductive invariance conserves and generates ordered structures. However, despite the properties of teleonomy and reproductive invariance, species still evolve and this point is fundamental for life.
This occurs mainly because of the effects of chance, accidental mutations on invariant teleonomic structures, able to conserve the DNA mutations and therefore keep what came about by pure chance in the genetic code which in some conditions can create the phenomenon of serendipity, namely the capacity to find something, a solution for example, to an unknown problem.
Chance may also explain the alterations of the sequence of nucleotides that form the genetic code. Chance alterations can be preserved, reproduced and multiplied by the organism according to the need of teleonomy and reproductive invariance. This means that when a mutation is acquired by the genetic structure of the organism, it becomes a necessity. Evolution is the result of the combined effect of chance and necessity: the chance of variations and the necessity of the laws of natural selection that act on a macroscopic scale as a result of this we get robust structures i.e. able to keep their properties even if they are attacked.
Natural selection occurs through mutations that favour the development of organisms: each new mutation tends to alter this equilibrium and thus has more probability of being damaging, rather than useful. On the other hand, beneficial mutations allow the evolution of species. Consequently, over time, each species has progressively perfected its highly specialised genetic heritage. Each living organism makes up the final link in a chain of events that have taken place over approximately four billion years of evolution.
- Metabolism and enzymatic structures
Living organisms are extremely sophisticated chemical machines. In order to grow and reproduce they require biochemical reactions able to provide the essential elements for the cells. The metabolism of a single cell includes a complex set of reactions and is structured according to a large number of metabolic pathways (divergent, convergent or cyclical and even polycyclical) involved in anabolic and catabolic processes. Many important steps in cell metabolism are combined into reaction cycles, i.e. the Krebs cycle [7].
The single steps of the metabolic pathway are characterised by processes that for the most part take place in the presence of enzymes able to convert the substrate (reagent) into the product then used in turn as substrate to the enzyme involved in the next step. Thus, metabolic chains occur with sequential reactions, namely the product of the first reaction becomes the reagent in the second one, and where the product becomes the reagent in the third, and so on. A metabolic cycle may appear when the product in the final reaction of the process becomes the reagent of the first reaction.
In multistep processes (e.g. glycolysis) some reactions are in the steady-state conditions; the reaction rates rise or fall with substrate concentration. Other reactions are far from equilibrium; these steps are typically the key points of regulation for the overall pathway. Nevertheless, the coexistence of multiple steady-states leads to nonlinear effects, i.e. biochemical oscillations at the subcellular level.
As is known, the efficiency of an organism’s metabolism is guaranteed by the presence of enzymes able to act as catalysts and regulators in most biological processes: not only do they establish ionic and electrostatic interactions with the substrate, lowering the activation energy of the reactions, but they also recognise which substrate to bind with thanks to stereo-specificity of the catalytic site. The enzymes responsible for regulation are usually not simple enzymes but, rather, cooperative (allosteric) ones as their conformations are affected by the fixation of specific metabolites. The presence of this cooperativity, which induces conformational changes of the enzyme, is one of the main causes of nonlinearity in biological systems [7].
Enzymes are able to catalyse only one reaction, or very few similar reactions, as the active site interacts with reagents in a stereo-specific way and is also sensitive to small geometric or electronic structural differences. The binding energy that is established comes not only from possible covalent bonds, but also from a dense network of electrostatic interactions. As a consequence, cells are able to regulate their metabolism through many sophisticated mechanisms over a wide time scale (i.e. from less than a millisecond to days) either by modifying the activity of enzymes or by changing their abundance.
Finally, enzymes have relatively flexible structures, in which adsorption cavities and active centers continually change and adapt to the surroundings. According to the induced-fit theory [21], indeed, enzymes are dynamic and flexible structures and so their enzymatic cavities can be adaptable to substrates and environmental conditions.
- Conclusions
Biological systems typically show emerging collective behaviour thanks to non-linear interaction among the components. These systems reveal self-organising properties in that different parts tend to spontaneously organise themselves structurally, becoming progressively more ordered and differentiated. They also exhibit adaptive properties and are able to easily adapt to the environment. Biological systems, from bacteria colonies to more highly evolved organisms, have collective intelligence, a type of distributed and organized intelligence that has been present since the beginning of life on Earth. This concerns directly mankind as a polycyclical temporal hyperstructure which has a high level of collective intelligence.
References
[1] Hine R, 2008, A dictionary of biology (6th ed.) Oxford: Oxford University Press, 461.
[2] Helmreich EJM, 2001, Biochemistry of Cell Signalling, Oxford University Press, 368.
[3] Turing A, 1952, Phil. Trans. R. Soc. Lond. B, 237, 37-72.
[4] Wiener N, 1958, Nonlinear Problems in Random Theory, Wiley and MIT Press.
[5] Goldbeter A, Caplan SR, 1976, Annual Review of Biophysics and Bioengineering, 5, 449-476.
[6] Wallezcek J, 2000, Self-organized biological dynamics & nonlinear control, Cambridge University Press, 428.
[7] Nicolis G, Nicolis C, 2007, Foundations of complex systems, World Scientific Publishing, 247-274.
[8] Fudenberg D, Tirole J, 1991, Game Theory, MIT Press.
[9] von Neumann J, Morgenstern O, 1964, Theory of games and Economic Behavior, John Wiley Science Ed.
[10] Maynard-Smith J, Price GR, 1973, The Logic of Animal Conflict, Nature. 246, 5427, 15-18.
[11] Miller JH, Scott E, 2007, Complex adaptive systems: an introduction to computational models of social life, Princeton University Press.
[12] Lansing S, 2003, Complex Adaptive Systems, Annual Review of Anthropology, 32, 183-204.
[13] Wheeler WM, 2012, The ant-colony as an organism, J. Morphol., 22, 307-325.
[14] Marty F, 1934, Sur une généralisation de la notion de groupe, 8th Congress Math. Stockholm, 45-49.
[15] Vougiouklis T, 1996, New Frontiers in Hyperstructures, Hadronic Press,
Palm Harbor, 48.
[16] Isaeva VV, 2012, Self-organization in biological systems, Biology Bulletin, 2012, 39, 110-118.
[17] Sasaki T, Biro T, 2017, Cumulative culture can emerge from collective intelligence in animal groups, Nature Comm., 8:15049.
[18] Schrodinger E, 1944, What is life, Cambridge University Press.
[19] Nicolis G, Prigogine I, 1977, Self-Organization in non-equilibrium systems, Wiley-VCH, New York.
[20] Monod J, 2001, Il caso e la necessità, Milano, Mondadori.
[21] Koshland, 1994, The Key-Lock Theory and the Induced Fit Theory, Chem. Int. Ed. Engl., 33, 2375-2378.
