Le problème de Gardner connu aussi sous le nom de The Sultan’s Dowry Problem ou de Secretary Problem a été l’élément générateur d’un champ d’investigations dans le domaine du management. Il s’agit d’un problème de tri maximalisé sans retour qui met en évidence le problème de la stratégie à adopter. Nous allons dans un premier temps étudier une façon de l’aborder et ensuite commenter cette approche du point de vue stratégique.

Nous avons donc une liste à n éléments que nous parcourons de manière unique dans un sens sans possibilité de revenir en arrière et nous devons sélectionner l’élément maximal.

Pour résoudre ce problème nous pouvons utiliser la stratégie suivante. Nous examinons les m premiers éléments de la liste et nous sélectionnons ensuite le premier élément des éléments restants qui domine les m premiers.

Il existe deux catégories d’échecs de cette stratégie. La première provient de la présence de l’élément maximal dans les m premiers éléments. La seconde est générée par la présence d’un élément qui domine les m premiers éléments et qui se trouve avant l’élément maximal.

La probabilité pour un élément d’être élément maximal est égale à .

Si l’élément maximal se trouve à la position alors cette stratégie est toujours gagnante. Ainsi la probabilité devient . Si l’élément maximal se trouve à la position , il ne sera sélectionné que si l’élément dominant des premiers termes, se trouve dans les m premiers termes, ainsi la probabilité devient . Dans le cas générique, nous avons pour un élément maximal situé en , la probabilité égale à . Et si l’élément maximal est le dernier élément alors la probabilité qu’il soit sélectionné est égale à .

Comme il n’y a pas de possibilité de retour et que la sélection est unique les évènements sont exclusifs et les probabilités peuvent être additionnées. Nous obtenons ainsi l’expression suivante : .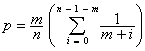

Comme la série harmonique tronquée en n est asymptotiquement équivalente à , pour n grand nous pouvons approximer par en posant que ce logarithme est unitaire pour m optimal, ainsi pour n grand la valeur optimale de m est égale à . Ainsi lorsque n est grand la probabilité est de l’ordre de .

Il existe un consensus dans le domaine que cette stratégie représente la meilleure possible mais en réalité cette démonstration se contente d’optimiser une stratégie donnée, elle ne démontre pas pour autant que celle-ci est la meilleure possible pour l’ensemble des stratégies possibles même si l’expérimentation numérique incite à penser cela.