- Erdös-Woods Numbers are defined as the length of an interval of consecutive integers whose every element is not coprime with its extremeties. Woods was the first to find such numbers, Dowe proved there exists an infinity and Cégielski, Heroult and Richard that their set is recursive. Our aim is to study the arithmetical proprieties of those numbers.
- First Erdös-Woods Numbers. (for d<=520 see Cégielski and al.)
16,22,34,36,46,56,64,66,70,76,78,86,88,92,94,96,
100,106,112,116,118,120,124,130,134,142,144,146,154,160,162,186,190,196,
204,210,216,218,220,222,232,238,246,248,250,256,260,262,268,276,280,286,288,292,296,298,
300,302,306,310,316,320,324,326,328,330,336,340,342,346,356,366,372,378,382,394,396,
400,404,406,408,414,416,424,426,428,430,438,446,454,456,466,470,472,474,476,484,486,490,494,498,
512,516,518,520,526,528,532,534,536,538,540,546,550,552,554,556,560,574,576,580,582,584,590,
604,606,612,616,624,630,634,636,640,650,666,668,670,672,680,690,694,696,698,700, 706,708,712,714,718,722,726,732,738,742,746,750,754,756,760,764,768,780,782,784,786,790,792,794,
800,804,806,814,816,818,820,832,834,836,838,844,846,852,862,870,874,876,880,886,890,896,
900,902,903,904,906,910,918,922,924,928,936,940,950,960,964,966,970,974,982,988,990,996,
1000,1002,1004,1008,1016,1026,1028,1030,1038,1044,1046,1056,1058,1060,1068,1074,1076,1078,1080,
1100,1106,1114,1116,1120,1122,1128,1134,1140,1144,1150,1158,1160,1170,1176,1180,1190,1196,
1200,1206,1208,1210,1212,1220,1222,1234,1240,1242,1246,1248,1254,1258,1262,1264,1268,1270,1272,1274,1282,1288,1294,1296,
1300,1310,1314,1318,1326,1330,1334,1338,1340,1342,1344,1350,1352,1354,1356,1358,1364,1372,1384,1386,1392,
1404,1406,1408,1412,1416,1418,1422,1438,1442,1446,1458,1462,1464,1470,1474,1476,1478,1480,1496,1498,
1502,1506,1508,1516,1518,1520,1526,1528,1530,1536,1540,1542,1546,1548,1552,1562,1564,1566,1574,1578,1590,1592,1596,
1600,1606,1612,1626,1630,1632,1640,1644,1650,1652,1654,1656,1662,1674,1676,1678,1680,1686,1688,1696,
1706,1716,1728,1732,1736,1740,1746,1750,1752,1758,1764,1766,1770,1772,1776,1780,1782,1792,1794,1796,
1800,1804,1806,1808,1818,1820,1826,1830,1834,1836,1838,1840,1842,1844,1856,1858,1860,1866,1870,1884,1892,1894,1898,
1900,1904,1910,1916,1918,1920,1924,1938,1940,1944,1948,1956,1958,1960,1962,1968,1978,1982,1986,1992,
2002,2010,2014,2016,2020,2022,2034,2038,2042,2044,2046,2048,2050,2052,2058,2066,2072,2074,2076,2078,2080,2086,2092,2094,
2102,2104,2106,2116,2118,2120,2122,2124,2134,2136,2140,2146,2148,2150,2152,2158,2160,2166,2168,2170,2172,2174,2176,2178,2184,2186,2190,2192,2196,
2200,2202,2216,2220,2226,2230,2232,2236,2248,2250,2254,2258,2262,2264,2278,2280,2284,2286,2292,
2300,2302,2304,2316,2318,2322,2328,2344,2346,2360,2362,2364,2368,2370,2376,2380,2386,2388,
2404,2408,2414,2420,2422,2426,2428,2430,2436,2440,2446,2450,2452,2454,2464,2466,2472,2482,2484,2490,2492,2496,2498,
2500,2502,2506,2508,2510,2514,2518,2520,2526,2530,2534,2538,2545,2546,2548,2560,2562,2568,2570,2574,2576,2586,2588,2590,2596,2598,
2604,2606,2612,2616,2620,2628,2640,2642,2652,2656,2662,2670,2676,2680,
2704,2706,2718,2724,2726,2728,2734,2736,2738,2740,2744,2746,2748,2752,2756,2760,2762,2766,2770,2772,2774,2780,2782,2786,2796,
2800,2808,2814,2822,2824,2826,2830,2832,2840,2850,2856,2860,2866,2868, 2870,2874,2878,2884,2886,2892,2894,
2900,2914,2916,2920,2922,2924,2946,2950,2952,2966,2976,2978,2982,2988,2990,2992,2994,
3006,3008,3014,3016,3018,3030,3032,3036,3040,3052,3054,3058,3060,3064,3066,3072,3078,3094,3096,3098,
3102,3108,3112,3114,3124,3130,3132,3140,3146,3148,3150,3154,3156,3162,3166,3174,3176,3180,3190,3198,
3200,3220,3228,3234,3240,3246,3248,3250,3264,3270,3276,3282,3284,3288,
3304,3306,3310,3318,3328,3334,3336,3346,3352,3354,3366,3368,3370,3378,3380, 3384,3388,3396,3398,
3402,3406,3410,3418,3420,3422,3430,3432,3436,3438,3440,3444,3454,3456,3472, 3474,3480,3486,3494,3498,
3504,3508,3510,3514,3516,3522,3524,3536,3538,3546,3552,3556,3568,3570,3574, 3586,3588,3590,3596,3598,
3600,3604,3610,3622,3630,3634,3636,3640,3648,3654,3656,3666,3668,3670,3680, 3682,3684,3688,3690,3694,3696,
3700,3708,3714,3716,3730,3732,3738,3744,3746,3750,3752,3760,3782,3784,3792,
3800,3810,3812,3816,3828,3830,3832,3836,3840,3846,3850,3868,3870,3872,3880, 3892,3894,
3900,3902,3904,3906,3910,3922,3926,3936,3938,3942,3960,3964,3978,3984, 3986,3996,
4000,4006,4010,4012,4016,4032,4034,4036,4038,4040,4042,4044,4046,4048, 4062,4068,4070,4086,4088,4098,
4102,4104,4106,4110,4116,4118,4122,4124,4146,4152,4156,4164,4170,4172,4174, 4180,4182,4186,4188,4190,4196,
4200,4204,4206,4208,4210,4224,4228,4238,4240,4248,4250,4256,4266,4270,4278, 4280,4286,4296,
4308,4312,4314,4316,4318,4320,4322,4324,4326,4332,4342,4344,4352,4354,4356, 4362,4368,4370,4378,4380,4382,4386,4394,4396,
4400,4402,4404,4412,4416,4418,4420,4428,4430,4434,4440,4444,4446,4468,4470, 4476,4478,4486,4488,4498,
4500,4506,4510,4512,4526,4530,4534,4536,4538,4540,4542,4546,4554,4560,4566, 4570,4572,4578,4580,4582,4588,4590,4594,4596
4602,4608,4610,4612,4620,4626,4628,4632,4646,4654,4656,4660,4662,4668,4670, 4678,4682,4684,4686,4688,4690,4698,
4700,4710,4718,4728,4732,4740,4746,4748,4750,4754,4758,4768,4770,4776,4782, 4792,
5184,6084,6494,6724,7056,7762,8100,8470,8472,8474,8476,8480,8484,9216,9988,9990,
10000,10404,11236,11638,11640,11664,12350,12544,14400,15876,16900,17424,22500,24336,26244,27556,29584,30276,31684,32400,36864,38416
44100,49284,51076,53824,56644,57600,71824,86436,93636,96100,
108900,112896,138384,142884,156816,166464,184900,191844,
207936,236196,240100,248004,252004,260100,270400,272484,315844,322624,324900,331776,
350464,357604,360000,396900
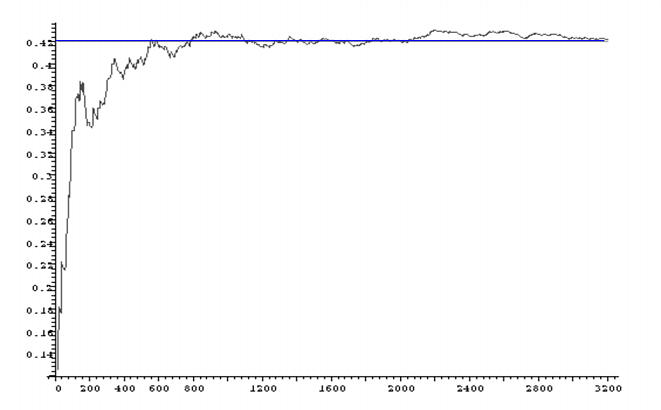
- DENSITY
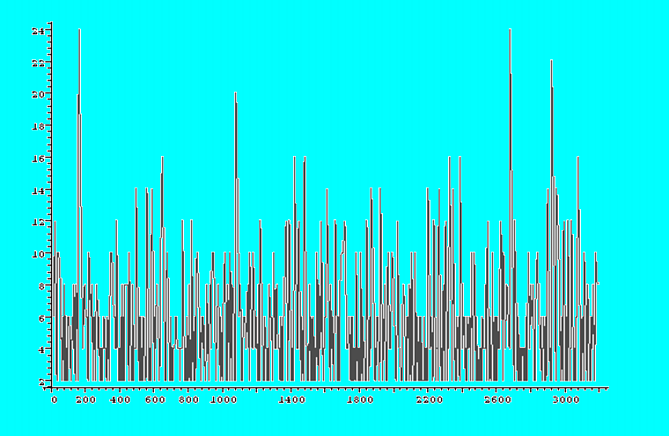
- CONSECUTIVE DIFFERENCE
- References :
P. Erdös, J.L. Selfridge : Complete prime subsets of consecutive integers. Proceedings of the Manitobe Conference on Numerical Mathematics. 1-14,1971
A. Woods : Thesis 1981
R. Guy : Unsolved Problems in Number Theory. 1981 (sections B27, B28, B29)
K. Lakki : Number Theory. 1984
D. Dowe : On the existence of sequences of co-prime pairs of integers. J. Austral. Math. Soc. Ser. A 47, no. 1, 84–89. 1989
P. Cégielski, F. Heroult, D. Richard : On the amplitude of intervals of natural numbers whose every element is coprime with no extremety. 2000


